1.1 Limit Superior and Limit Inferior
It is not always the case that the limit of a sequence exists — take \((a_n)_{n\in\mathbb{N}}\) defined by \(a_n = (-1)^n\), for example. But if a sequence \((a_n)_{n\in\mathbb{N}}\) is bounded, there are two objects that always exist. These are the limit superior and limit inferior of a sequence. To start define these, we first let \((a_n)\) be a real sequence, and for each \(k \in \mathbb{N}\), define \[A_k = \lbrace a_n \,\lvert\, n \geq k\rbrace = \lbrace a_k,\,a_{k+1}\,\ldots\rbrace\]
We also use some different notation to describe the supremum and infimum of the sets \(A_k\), namely 1 \[\sup A_k := \sup_{n\geq k}a_n \quad ; \quad \inf A_k := \inf_{n \geq k}a_n.\] One thing we can say about these quantities is that since \(A_{k+1} \subseteq A_k\), we know that \((\sup A_k)_{k\in\mathbb{N}}\) is a decreasing sequence, and \((\inf A_k)_{k\in\mathbb{N}}\) is an increasing sequence. Now that we’ve produced two new sequences, the natural thing to do is analyse their convergence. It turns out that if \((a_n)_{n\in\mathbb{N}}\) is bounded, both \((\sup A_k)_{k\in\mathbb{N}}\) and \((\inf A_k)_{k\in\mathbb{N}}\) converge! We define their respective limits to be 2 \[\limsup_{n \to \infty} a_n := \lim_{k\to\infty}\sup_{n\geq k}a_n \;\, \text{and} \;\, \liminf_{n \to \infty} a_n := \lim_{k\to\infty}\inf_{n\geq k}a_n.\] The first of these is the limit superior and the second is the limit inferior. These can be thought of as `eventual’ bounds on a sequence, as seen in Figure 1.1 (Taken from Wikipedia).
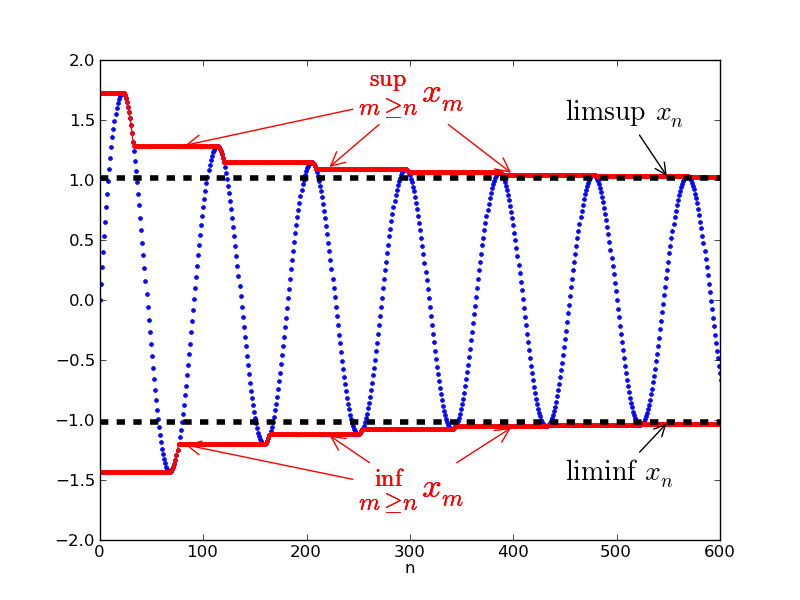
Figure 1.1: Limsup and liminf for a sequence.
There is also another way of interpreting the limits superior and inferior. For a sequence \((a_n)_{n\in\mathbb{N}}\), we can also think of \(\limsup_{n\to\infty} a_n\) and \(\liminf_{n \to \infty}a_n\) as being the largest and smallest possible limits of any subsequence of \((a_n)_{n\in\mathbb{N}}\). We can use this to characterise convergent sequences!
A sequence \((a_n)_{n\in\mathbb{N}}\) is convergent if and only if \[\limsup_{n \to \infty} a_n = \liminf_{n \to \infty} a_n.\]
To end this section, we state two more results. They’re not mentioned in the lecture notes, but they can be incredibly useful when performing calculations3.
Let \((a_n)_{n\in\mathbb{N}}\) and \((b_n)_{n\in\mathbb{N}}\) be real sequences. Then: \[\limsup_{n\to\infty}(a_n + b_n) \leq \limsup_{n\to\infty}a_n +\limsup_{n\to\infty}b_n,\] and \[\liminf_{n\to\infty}(a_n + b_n) \geq \liminf_{n\to\infty}a_n +\liminf_{n\to\infty}b_n.\]
The notation here follows that used in the lecture notes rather than that used in lectures, as this is more common usage. Also, for convenience, if the set \(A_k\) is not bounded above/below, we set the supremum/infimum to be \(\infty\)/\(-\infty\).↩︎
Again, if \((\sup A_k)_{k\in\mathbb{N}}\) diverges to \(\infty\), \(\limsup_{n \to \infty} a_n\) is defined to be \(\infty\), and if \((\inf A_k)_{k\in\mathbb{N}}\) diverges to \(-\infty\), \(\liminf_{n \to \infty} a_n\) is defined to be \(-\infty\).↩︎
Since these results are not in the lecture notes, it’s highly recommended that you try and prove them yourself. Try using similar techniques to Tutorial Question 2 on Problem Sheet 7 and Homework Question 6 on Problem Sheet 3.↩︎